If you like this blog post, do subscribe to my RSS feed

What do Kirchhoff, Cayley, and Carroll have in common? And who is Kahrimanian?

Author: Parth Parikh

First Published: 26/02/23

The Lorax: Which way does a tree fall?
The Once-ler: Uh, down?
The Lorax: A tree falls the way it leans. Be careful which way you lean.
- Dr. Seuss, The Lorax

All four individuals made interesting early contributions to a mathematical structure that we now know as a tree. In this blog post, we will briefly explore their unique contributions and see how the tree structure was introduced in both mathematics and computer science.

If you find any inaccuracies in this blog post, please do let me know.

Gustav Kirchhoff and Karl G. C. von Staudt

Before we dive into Kirchhoff’s contribution, let us review what a free tree and a fundamental cycle are.

A free tree is a connected graph with no designated root and no cycles, hence its alternate name, an unrooted tree. This distinguishes it from an arborescence, which consists of a designated root node.

Although there are many intuitive definitions of a fundamental cycle, one of the simplest comes from Casteels on Math Exchange:

Let \(G\) be a connected graph, and let \(T\) be a spanning tree of \(G\). Let \(e\) be an edge in \(G\) between vertices \(v\) and \(w\) that is not in \(T\). Now in \(T\) there is a unique path between \(v\) and \(w\), and since \(e\) is not in \(T\), that path does not use \(e\). Therefore, that path together with \(e\) forms a cycle in \(G\). A cycle built this way is called a fundamental cycle.

Here is a neat visualization of the same:

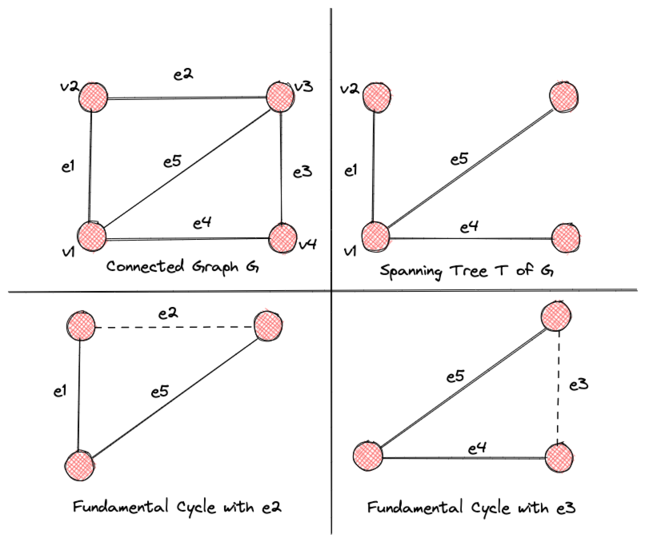
So, what is the relation between free trees, fundamental cycles, and Gustav Kirchhoff? Well, as mentioned in Donald Knuth’s TAOCP Volume 1, Gustav Kirchhoff was one of the first to use free trees to find a set of fundamental cycles in an electrical network. His 1847 paper also formed the basis for the now ubiquitous Kirchhoff’s current and voltage laws.

Kirchhoff used \(m\) to denote the number of junctions (nodes) and \(n\) to denote the number of branches (edges). While stating Theorem 2, he mentioned the equation \(\mu = n - m + 1\), which finds the number of fundamental cycles in a graph \( \mu \). Furthermore, the number of equations needed for Kirchhoff’s Voltage law (Theorem 1 in the paper) is given by the least number of edges that must be removed from the graph for all the cycles to be destroyed.

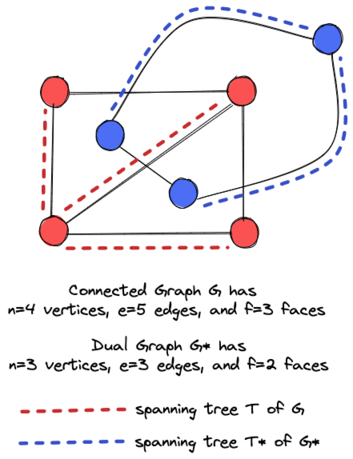
Interestingly, Donald Knuth also cites Karl G. C. von Staudt’s 1847 work Geometrie der Lage (pages 20 and 21) as an early contribution to the field of trees. In his work, von Staudt showed proof of Euler's polyhedron formula, \( n - e + f =2 \), where \(n\) is the number of vertices, \(e\) is the number of edges, and \(f\) is the number of faces. Euler mentioned his result in a letter to Christian Goldbach in 1750; however, he did not give the first correct proof of his formula. The French mathematician Adrian Marie Legendre is often cited as having given the first correct proof of this formula, somewhere in 1794.

So, what was von Staudt’s contribution? As it turns out, von Staudt presented proof of Euler's polyhedron formula that relied on the use of trees. Although the original text is in German, Robin Whitty has neatly summarized the proof in one of his "Theorem of the Day" posts:

For graph \(G\), take the dual graph \(G*\) whose vertices are the plane faces and whose edges join dual vertices by crossing edges of \(G\). Take a spanning tree \(T\) in \(G\): it has \(n\) vertices and \(n - 1\) edges. The remaining edges of \(G\) are crossed by a spanning tree \(T*\) of \(G*\): it has \(f\) vertices and \(f - 1\) edges. Every edge of \(G\) is in \(T\) or is crossed by an edge of \(T*\). So \(e = (n - 1) + (f - 1)\).

A visualization of this proof is shown in Figure 2.

Arthur Cayley

It was not until ten years later, in 1857, that Arthur Cayley formulated the term "tree" in his paper "On the theory of the analytical forms called trees." Over three decades (1857-89), he published a series of papers on the theory of trees and their applications. As stated by Donald Knuth, Cayley seemed to be unaware of the previous work of Kirchhoff and von Staudt. His investigations mainly involved the study of isomers in chemistry and the structure of algebraic formulas.

Cayley’s 1857 contribution was using trees as an organizational tool for differentiation. This is succinctly expressed by Prof. Gerald M. Lodder at NMSU:

In an 1857 publication [9], Cayley introduces the term “tree” to describe the logical branching that occurs when iterating the fundamental procedure of differentiation. Calculus is not the main concern here, but instead an organizational tool is developed that provides a visual overview of the individual terms under differentiation. This tool is used today in quite different situations from networks in computer science to finding efficient delivery routes in the transportation industry. To introduce Cayley’s paper, let \(\partial_x\) denote differentiation with respect to \(x\) and let \(\partial_y\) denote differentiation with respect to \(y\). Then \(\partial_x(x^2 y) = 2xy\) and \(\partial_y(x^2y) = x^2\), given that \(x\) and \(y\) are independent variables. The symbols \(\partial_x\) and \(\partial_y\) are called operators, while the expression \(x^2 y\) itself is an operand. Note that the symbols \(\partial_x\) and \(\partial_y\) are applied to (operate on) functions written to the right of the symbol. If the function is written to the left, such as \(x^2 y \partial_x\), Cayley dubs the entire expression an operandator, and \(x^2 y\) remains unaltered by the operator on the right. Cayley wishes to study how operandators interact among themselves. Let \(P = x^2 y \partial_x\) and \(Q = xy \partial_y\). Then PQ is the operandator given by \[PQ = x^2 y \partial_x(xy \partial_y) = x^2 y(y \partial_y) = x^2y^2\partial_y\] and \(QP\) is the operandator given by \[QP = xy \partial_y(x^2y \partial_x) = xy(x^2\partial_x) = x^3y\partial_x\] In the above example, \(QP \ne PQ\). For operandators \(Q\), \(P\), \(U\), what should be the meaning of \(QPU\)? Do the groupings \(Q(PU)\) and \((QP)U\) yield the same result, with \(Q\), \(P\), and \(U\) are in the same relative order?

Here is the relevant part from Cayley’s 1857 paper:

Later, in 1874, Cayley published another paper wherein he used trees to enumerate the isomers of compounds of form \(C_n H_{2n+2}\).

Lewis Carroll

Charles Dodgson, better known by his pen name Lewis Carroll, made a fascinating observation in the theory of trees. In 1972, W. W. Bartley \(III\) published a paper on Carroll's lost book on logic, which contained the Method of Trees, one of the earliest uses of truth trees to prove or refute a logical formula.

Nowadays, truth trees are widely used to prove theorems, analyze the logical structure of mathematical proofs, and formalize the rules of grammar in artificial intelligence and linguistics. While discussing the Method of Trees, W. W. Bartley \(III\) writes the following:

METHOD OF TREES was developed by Dodgson as a means of testing the validity of a conclusion derived from premises. It is strikingly similar to the "trees" frequently used by contemporary logicians. The basic idea is to assume that the premises are true but the conclusion is false (and its denial is true). If combining the denial of the conclusion with the premises leads to an absurdity, it shows that the premises do indeed prove the conclusion. The explanation here has been reset from the section describing "The Method of Trees " in Dodgson's unpublished work. It deals with a simple tree that does not require branching.

Interestingly, in his discussion of the Method of Trees, W. W. Bartley \(III\) notes that Lewis Carroll applied this method to the Crocodile dilemma in his unpublished work.

A curious reader can explore more about Carroll’s approach in Bartley’s paper.

H. G. Kahrimanian

Donald Knuth mentions something fascinating in TAOCP about the history of trees in computer science:

Tree structures represented explicitly in computer memory were originally used for applications to algebraic formula manipulation. The machine language for several early computers used a three-address code to represent the computation of arithmetic expressions; the latter is equivalent to the INFO, LLINK, and RLINK of a binary tree representation. In 1952, H. G. Kahrimanian developed algorithms for differentiating algebraic formulas represented in an extended three-address code; see Symposium on Automatic Programming (Washington, D.C.: Office of Naval Research, May 1954), 6–14.
Since then, tree structures in various guises have been studied independently by many people in connection with numerous computer applications .....

This might make H. G. Kahrimanian's 1952 paper one of the earliest references to a tree-like structure (in guise) in computing. Interestingly, for a long time, I thought that his thesis was lost. Then a few months back, I came across the proceedings of the 1954 Symposium on Automatic Programming on Google Books. And sure enough, inside it was Kahrimanian’s paper Analytical Differentiation by a Digital Computer.

Little is known about Harry G. Kahrimanian beyond the fact that he completed his Master's thesis at Temple University in 1953 and later worked at the Naval Aviation Supply Office in Philadelphia, Pennsylvania. However, Kurt W. Beyer's book Grace Hopper and the Invention of the Information Age contains fascinating information about him:

Hopper had the habit of assigning the most difficult technical problems to the youngest and least experienced members of a team. Mildred Koss, shortly after arriving at the Eckert-Mauchly Computer Corporation, was handed the task of having the UNIVAC automatically edit its data for printing. The result was Koss’s “editing generator,” a sophisticated piece of code that created margins, titles, headings, and page numbers on the fly and represented the first attempt to use a computer for word processing. Harry Kahrimanian, just out of college, got an even more daunting assignment: he was asked to create a program that could automatically solve differential equations. Kahrimanian’s differentiator was a watershed in applied mathematics. The user had merely to enter the equation and indicate the number of n derivatives; the computer did the rest. Kahrimanian’s achievement was even more impressive in light of Hopper’s own long and arduous experience working alongside the famed mathematician John von Neumann to solve differential equations on the Harvard Mark I. Had Kahrimanian’s differentiator been available to von Neumann and Hopper, they could have solved the Manhattan Project’s implosion problem in days instead of months.

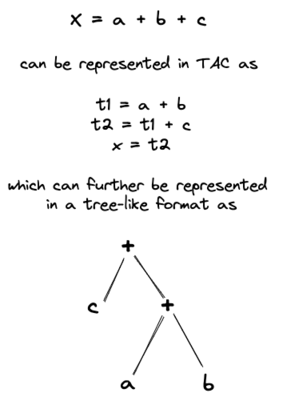
To understand Kahrimanian's contribution to trees, it's important to first understand Three-address codes (TAC), which is an intermediate representation of a program that uses at most three operands to represent an operation. TAC can be represented as a tree-like structure where the nodes represent the operands and operators, and the edges represent the flow of data between them. For instance,

For Kahrimanian's differentiator system, he defined a symbolic language to express elementary functions and their derivatives using three-address code expressions like:

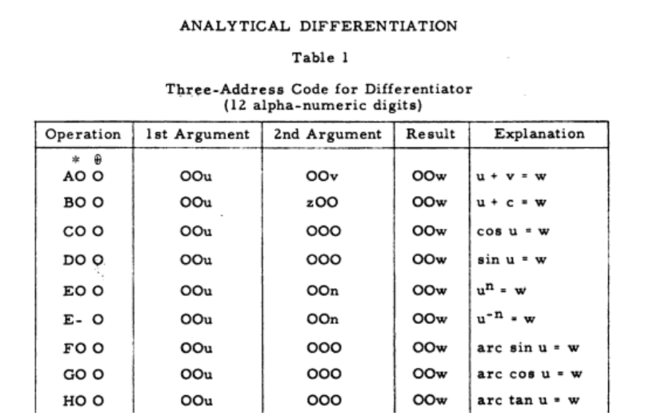
These expressions were then used to define a function in three-address code, which in turn could be represented as a tree-like structure.

However, it's worth noting that Kahrimanian did not use the term "tree" in his paper to describe these structures.

Lastly, Donald Knuth had the following to say about the explicit mention of trees in the early days of Computer Science:

Since then, tree structures in various guises have been studied independently by many people in connection with numerous computer applications, but the basic techniques for tree manipulation (not general List manipulation) have seldom appeared in print except in detailed description of particular algorithms. The first general survey was made in connection with a more general study of all data structures by K. E. Iverson and L. R. Johnson [IBM Corp. research reports RC-390, RC-603, 1961; see Iverson, A Programming Language (New York: Wiley, 1962), Chapter 3]. See also G. Salton, CACM 5 (1962), 103–114.

Conclusion

And that’s it, folks! I hope you enjoyed this little adventure I took you on today. We spend most of our lives trying to learn the what and the why of our fields, but it is nice to stop once in a while and ask ourselves: how did we achieve all of this, who was responsible for it, and what problems were they initially trying to solve?

Make no mistake, I am sure that I have missed exploring many contributions. However, I encourage curious readers to further explore the various citations I’ve sprinkled throughout this blog. Who knows? You might find some treasures in the works of Borchardt, Listing, Jordan, and Borůvka.

←