Turn on/off lights

Spectral Bloom Filters for Client-Side Search

Behind every great program is a great data structure.
This June, a fascinating blog-post appeared on Hacker News' frontpage - Writing a full-text search engine using Bloom Filters (2013). Articulated by Stavros Korokithakis, this blog-post brought a new perspective to the client-side search problem - "Bloom Filters" was the cry. While this unique thought paved the way for libraries like Tinysearch, it brought with it a pressing concern - how do we rank these documents?

To start, let us ask ourselves a fundamental question, what would a perfect search solution for any static website look like? It would naturally be space-efficient (in both compressed and non-compressed form), have a satisfactory ranking involved, and would not send any server-side requests. While solutions like Google Custom Search provide a degree of flexibility and ease-of-use, their proprietary nature together with the fact that they bundle ads with their free version indisputably puts them on backfoot. Progressing with a torch labeled client-side search, we soon notice a dilemma. How can a search solution be both memory efficient and provide cogent ranking? To paint a picture, I am talking about a search engine capable of indexing and ranking hundreds of documents using KBs or at most a few MBs of memory.

While Mr. Korokithakis's blog-post coherently dealt with the size concern, a glaring weakness he mentioned was:

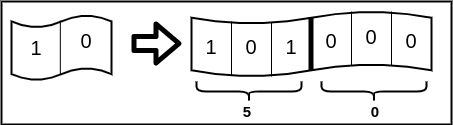
You can’t weight pages by relevance, since you don’t know how many times a word appears on a page, all you know is whether it appears or not.
Placing our primitive Bloom Filters under a microscope, we realize that stretching our Bloom Filters seems like a creative solution to this problem. More technically, by replacing all the one-bit indices of a primitive Bloom Filter with counters of width w, we can introduce the ability to store frequencies for each token (or word) (Figure 1). Furthermore, these counters of width w will consume w×m bits of memory (where m is the number of counters) and can store a maximum frequency of 2w−1. However, as Bloom Filters are probabilistic in nature and carry with them a certain false positive error (E), we arrive at yet another pertinent question - what new error have we introduced by using counters and how do we minimize this error? In enters Spectral Bloom Filters.

The conversion of one-bit indices of a primitive Bloom Filter to counters of width w=3.
Figure 1: The conversion of one-bit indices of a primitive Bloom Filter to counters of width w=3. The first counter in the figure stores a value of 5 whereas the one to its right has count=0.

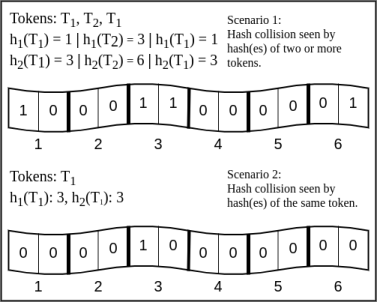
Before we dive in, let us understand the error we introduced by using counters. Count mismatch error occurs when the frequency of a token in a Bloom Filter differs from its actual frequency in the document. Figure 2 describes the two scenarios when a count mismatch can occur.

The two scenarios when a count mismatch can occur.
Figure 2: In scenario 1, as T1 and T2 both hash at index 3, a severe case of count mismatch is observed, with T1 and T2 off by values 1 and 2 respectively. Moreover, in scenario 2, as two similar hash indices are generated for T1, an implicit collision takes place. While scenario 2 can easily be overcome using larger m, scenario 1 requires us to look at this problem from a different perspective.

Introduced by Saar Cohen and Yosi Matias, Spectral Bloom Filters (or SBFs) is a variant of the above counter-like Bloom Filters. To reduce the number of count mismatches and false-positive error rates, three concepts were established in their paper: minimum selection, minimal increase, and recurring minimum. The minimum selection algorithm is based on a principle that while querying for a token T, the minimum value amongst all hashed indices is the closest estimate for the frequency of T. That is, for counters C1, C2, ..., Cm, the frequency of a token T can be estimated as freq(T) = min(Ch1(T) , Ch2(T) , ..., Chk(T)) , where k is the number of hash functions. In addition, the minimal increase algorithm argues that in order to reduce count mismatches (as seen in Figure 2, scenario 1), only the counters possessing the minimum value should be incremented. However, one must note that performing deletions with minimal increase at the core can cause false-negative errors. To counter the false-negative errors and add in a deletion functionality, the authors suggested the recurring minimum algorithm. Figure 3 shows an example of the Minimal Increase algorithm.

A working example of a Spectral Bloom Filter created using Minimal Increase algorithm.
Figure 3: A working example of a Spectral Bloom Filter created using Minimal Increase algorithm.

For client-side search, we ideally need an algorithm capable of supporting insertions while keeping false positive error and count mismatches in check. Deletions would be a superfluous operation as websites when updated can always rebuild their Spectral Bloom Filters to reflect the new changes. Removing deletion operation can significantly reduce the size of the filters as the recurring minimum (although not explained in this blog-post) requires a secondary Spectral Bloom Filter for performing the deletion.

Based on the above analysis, I, along with my colleagues (Mrunank Mistry and Dhruvam Kothari) designed the library - Sthir which performs client-side searching using Spectral Bloom Filters with minimal increase algorithm revolving around its nucleus. A demo of our library can be found on this very blog. 😊

Our library uses a TF-IDF based approach for ranking and a home-grown technique called base2p15 for encoding. Our paper was recently accepted at the 11th IEEE Annual Information Technology, Electronics, and Mobile Communication Conference, Vancouver, 2020. As the paper is yet to be indexed on IEEE Xplore, I am unable to provide a DOI of the same.

Edit (24/12/20) - Our paper got indexed on IEEE Xplore. DOI: https://doi.org/10.1109/IEMCON51383.2020.9284946. Furthermore, if you would like to read our draft, please feel free to drop me an email.
←