Pseudocode to Code Generation

Integrating code analysis and synthesis with Natural Language Processing can open doors for many interesting applications like generating code comments, pseudocode from source code and UML diagrams, helping search code snippets, creating rudimentary test cases, improving code completion, and finally synthesizing code from pseudocode. Based on [1], the techniques to perform the above applications ranges from NLP tools such as POS tagging, language parsers, and word embeddings to sophisticated deep learning models.

Fascinated with the above use-cases, I decided to explore the research cultivated in this domain. To narrow down my focus, I started with pseudocode to code generation. Earlier this year, a demo of an OpenAI language model applied to code generation was published on Twitter (starts around 28:00) -

We've talked about how these massive language models trained on supercomputers can do all these different kinds of natural language tasks, but the models actually go much further. When we fine-tune them on specific data, we find that they can do things that we didn't expect. And one thing we were curious about was what we could do with code-generation. Could we help developers write code? And so, we used the Microsoft supercomputer, our generative text models, and we fine-tuned it on thousands of open source Github repositories. - Sam Altman

The examples provided in the above demo were astounding, to say the least. As mentioned, their goal seems to be about improving the creative aspects of coding by automating mundane tasks.

To dive deeper, I read two recent papers which throw more light into the implementation aspect, albeit on a smaller scale as compared to OpenAI. SPoC: Search-based Pseudocode to Code (2019) [2] presents a new dataset for this task. This dataset contains around ~18,000 C++ programs collected from competitive programming sites such as Codeforces. The paper mentions that there are on average 14.7 lines per program, which are all human-annotated by crowdsourcing it on Amazon Mechanical Turk. As the dataset presents test-cases, the synthesized program is said to be accepted if it passes all the public and hidden test cases. Here is how the training data looks like -

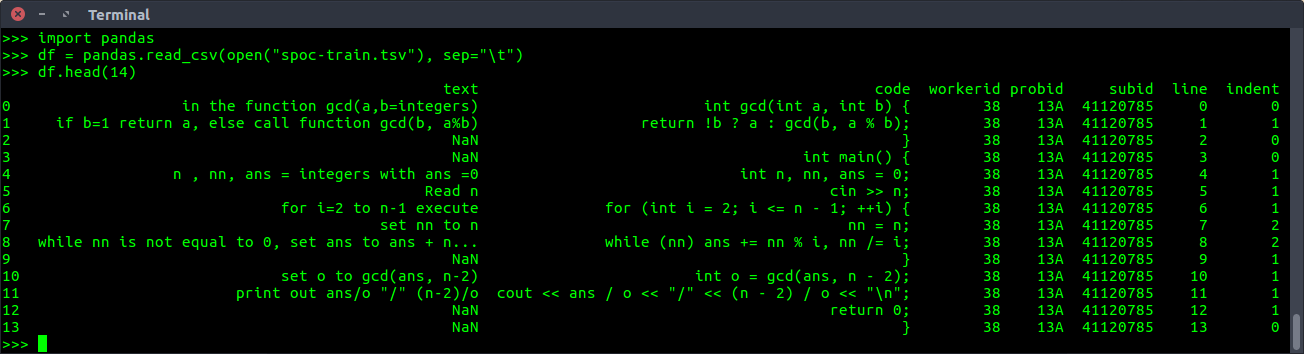
Apart from the annotations and code lines, there is information about the line numbers, indentation levels, and the probid, which appears to be a unique id for the test cases. We can also use the above probid to query the relevant Codeforces question - https://codeforces.com/problemset/problem/13/A.

The main task as concisely defined in their paper is the following -

Given (a) a sequence x of L pseudocode lines x₁, x₂, ..., x_L and (b) k public test cases in the form of input-output string pairs (T₁ⁱⁿ, T₁^out), ..., (T_kⁱⁿ, T_k^out), the task is to synthesize a program y consisting of L code lines y₁, y₂, ..., y_L. Each code line y_i is a fragment of code whose semantics is described by the pseudocode line x_i.

In simple terms, we use each pseudocode line to generate its corresponding code line and continue to do this for all lines. After the program is generated, we verify it using the public and hidden test cases. For training, the authors have provided the data in the above table along with its corresponding public and hidden test cases. However, the testing is primarily performed using the pseudocode lines and the public test cases. In both the papers (the other being [3]), the authors have further provided a computational budget, with one unit equivalent to the execution and validation of a single compiled program. As mentioned in the Introduction section of [2]:

Using the top-one translation of the pseudocode yields a success rate of 24.6% on the test set. Under a limited budget of 100 synthesis trials (i.e., 100 code compilations and executions), our best method achieves a success rate of 44.7%.

So what is this best method? And how is it nearly doubling the success rate?

To start, let me first explain the meaning of a top-one translation. Observe the table shown below -

In the above table, for simplicity, three probable candidates of each pseudocode line are shown. These are ordered as per their probability, so candidate 1's are predicted to be more probable than 2 and 3. Top-one translation is when all the candidate 1's are combined into a single program, to be compiled and executed. If an error is seen during the compilation or execution phase after top-one translation, we move on to the next combination of candidates. The authors propose a best-first search approach for this. But what is this best-first search?

From Artificial Intelligence: A Modern Approach (3rd edition, page 92) -

Best-first search is an instance of the general TREE-SEARCH or GRAPH-SEARCH algorithm in which a node is selected for expansion based on an evaluation function, f(n). The evaluation function is construed as a cost estimate, so the node with the lowest evaluation is expanded first.
The choice of f determines the search strategy. Most best-first algorithms include as a component of f a heuristic function, denoted h(n):
h(n) = estimated cost of the cheapest path from the state at node n to a goal state.

Dijkstra's algorithm can be considered a more general idea of best-first search as it does not use any heuristic function. By using a heuristic function, although we are not guaranteed to find the shortest path, the time taken to find the goal will be much quicker when compared with Dijkstra's algorithm. A^* is a variant of the best-first search with the following heuristic function -
f(n) = g(n) + h(n);
where g(n) is the cost to reach the node and h(n) is the cost to reach from that node to the goal node. We usually implement the best-first search using a priority queue. For our implementation, the authors suggest using a heap. This heap will initially contain the top-one translated program. For each iteration, a pop() operation is performed and the program obtained is compiled and executed. If an error is found (or test mismatches have occurred), modified programs (using the next candidate combinations) are then pushed into this heap. The process stops when we find a solution or exhaust the search space. As rightly mentioned in paper [3], if we use a priority queue, to find the top B highest-scoring candidates, we would require O(L*log(BL)) per candidate, where L is the number of lines in the synthesized program.

However, can we improve the heuristic function? Well, our basic instinct suggests that when we find an error, we fetch its line error, and move to the next candidate for that line. This pruning can significantly reduce the search space. However, as paper [2] mentions -

Unfortunately, the reported line numbers do not always correspond to the actual location of the mistake (e.g., the error 'n was not declared in this scope' can occur long after the line where n should be declared according to the pseudocode). Empirically, the reported line number does not match the actual incorrect line 21.7% of the time.

To solve the above problem, the authors propose multiclass classification and prefix-based pruning. The multiclass classification uses pseudocode lines, synthesized code lines, and error messages as an input to an error correction model [4] which then predicts the offending line. However, the authors state that the multiclass classification method does not guarantee that the predicted line is causing the error. To combat this, they use additional compiler calls to find a group of concurrent lines that fails the program's compilation. They maintain a maximum offset of 2 lines to limit the search space. The susceptible lines can then be blacklisted altogether or their candidate probability can be reduced. Here are the results observed by the paper [2] -

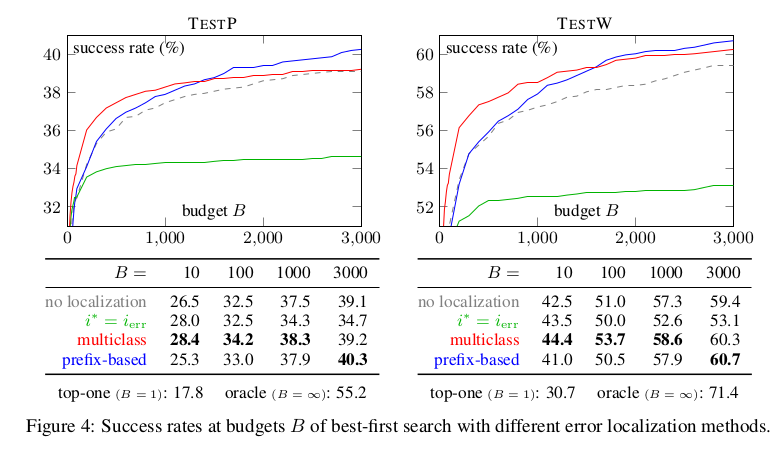
The authors have divided their work into two test sets - TestP and TestW. TestP was obtained by holding out 23% of their problems (total was 677), and the TestW was formulated by holding out the work of 7 Mechanical Turk workers (out of a total of 59). I believe there is an error either in paper [2]'s abstract or introduction. In the abstract, they mention the top-one success rate to be 25.6%, however, in their introduction, (paragraph 7 line 1) they mention the error to be 24.6%. Nevertheless, an interesting observation they found was -

Prefix-based pruning slightly increases the number of compilations for easier problems, but is more effective on harder programs, making it outperform the multiclass classifier under larger budgets.

How is the machine translation system to generate candidate code lines working?

To generate candidate code lines, we use the standard seq2seq implementation from OpenNMT with an LSTM encoder and decoder, attention-based copying mechanism, and coverage vector.

As I have yet to explore the relevant papers for machine translation, I am unable to provide more insight into this working. Another recent paper Semantic Scaffolds for Pseudocode-to-Code Generation [3] made an interesting observation, i.e. to generate programs that can be executed correctly, we need to consider both the syntactic (grammatical specifications) and semantic (such as the scope of the variables) nature of the candidates. For example, in figure 2 above, line 5's candidate 1 misses the curly braces ({), moreover, (line 4 - candidate 1) reinitializes the i^th variable (it was first initialized on line 2). While the latter prevents a logical bug due to the absence of tampering of variable i between lines 2-5, the former can cause a compile-time error. Therefore, the best-first search's heuristic must understand the syntactic and semantic nature of the candidates.

The authors of paper [3] made three important observations. First, to enforce syntactic constraints, we can extract the grammar symbols from the candidate code and use an incremental parser to check if the grammar symbol combination is a derivation of an abstract syntax tree. Incremental Parsing is thoroughly explained in [5] and in the book Recent Advances in Parsing Technology [6] (chapter 2). Second, a variable table can be used to keep a log of the scope of each variable, minimizing the undeclared/redeclared variables' semantic errors. To find a working combination of candidates given the above constraints, the authors propose a beam search implementation. As succinctly mentioned on Wikipedia -

Beam search is an optimization of best-first search that reduces its memory requirements. Best-first search is a graph search which orders all partial solutions (states) according to some heuristic. But in beam search, only a predetermined number of best partial solutions are kept as candidates.

Beam search uses breadth-first search to build its search tree. At each level of the tree, it generates all successors of the states at the current level, sorting them in increasing order of heuristic cost. However, it only stores a predetermined number, β, of best states at each level (called the beam width). Only those states are expanded next. The greater the beam width, the fewer states are pruned. With an infinite beam width, no states are pruned and beam search is identical to breadth-first search.

By enforcing the above constraints, the authors observed that while it improves the program accuracy, for large beam width (>=1000), the time complexity of the beam search grows considerably. In order to further reduce this time complexity, the authors presented their third important observation - scaffolds. The authors have defined a scaffold as an abstraction of syntactic and semantic information. For example, val+=2 and val=val+2 mean the same (both syntactically and semantically). Therefore such candidates if proposed can be abstracted into a single candidate. This reduces redundant computations. Therefore, we can then apply beam search on these abstractions first, and then expand the chosen candidates before compilation. The probability of abstraction can then be the total of the individual candidates' probability.

Code generation is truly a breathtaking subject. I am planning to explore a different tangent in a few days - Inductive Program Synthesis, starting with the famous FlashMeta paper which explains the FlashFill algorithm (Ctrl + E) used by Microsoft Excel. Will update the blog soon! Happy Exploring!

References

[1] Natural Language Processing Techniques for Code Generation, Hendrig Sellik, URL: https://repository.tudelft.nl/islandora/object/uuid:3a6625b0-21da-4746-bab3-f409eed93f30/datastream/OBJ/download
[2] Kulal, Sumith, et al. "Spoc: Search-based pseudocode to code." Advances in Neural Information Processing Systems. 2019. URL: https://arxiv.org/abs/1906.04908
[3] Zhong, Ruiqi, Mitchell Stern, and Dan Klein. "Semantic Scaffolds for Pseudocode-to-Code Generation." arXiv preprint arXiv:2005.05927 (2020). URL: https://arxiv.org/abs/2005.05927
[4] Gupta, Rahul, et al. "Deepfix: Fixing common c language errors by deep learning." Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence. 2017. URL: https://www.aaai.org/ocs/index.php/AAAI/AAAI17/paper/viewFile/14603/13921 (This paper by IISc graduates looks interesting, will update this post when I finish exploring it)
[5] Ghezzi, Carlo, and Dino Mandrioli. "Incremental parsing." ACM Transactions on Programming Languages and Systems (TOPLAS) 1.1 (1979): 58-70.
[6] Bunt, Harry, and Masaru Tomita, eds. Recent advances in parsing technology. Vol. 1. Springer Science & Business Media, 1996.

←