Turn on/off lights

Understanding Computational Complexity

As an initiative to make this blog more accessible, I have added an audio version of this article.

What is a problem ?

An inquiry starting from given conditions to investigate or demonstrate a fact, result, or law.

With problems posed as questions, we seek answers. I remember back when I was 5 or so, a camel standing across the street caught my curiosity. I observed that camel for a very long time thinking why the hell won't it sit down and if it did, which side would it sit on ( left or right leaning ). The nature of these problems makes us wonder, how to solve them efficiently ? But can we solve all imaginable problems efficiently ?

In computer science, problems are divided into decidable and undecidable problems. Decidable problems are the ones for which we can always construct some algorithms to answer correctly. Solving Fibonacci sequence is a decidable problem as this algorithm would indicate fib[n] = fib[n-1] + fib[n-2] with predefined values fib[0] = fib[1] = 1. Undecidable problems are ones for which no algorithm exists which can always answer correctly.

To give some perspective into undecidable problems, let's look at the legendary Halting Problem. The problem states that given an arbitrary computer program and an input, can we determine whether this program would run forever or halt after some time. To understand why this problem is undecidable, try analyzing the following pseudo-code:

def Deceiver(i):
  oracle = i[0]
  in = i[1]
  if oracle(Deceiver, i):
	while True:
	  continue
  else:
	return i

If the Oracle says the program will halt, an infinite loop is executed. If it answers negatively, we halt the program. No matter what Oracle says, we perform the opposite action. You can read more about this perspective here.

Let's look at two classes of problems before we continue further: decision problems and optimization problems. I like to think of decision problems as ones with a yes/no type answer and optimization problems as ones where MIN or MAX of a state is to be determined.

With these definitions explained, let's now look at P, NP, NP-Complete and NP-Hard complexity classes. A small terminology before we continue further, polynomial time complexity ( in terms of big-O notation ) -> n^O(1).

P can be explained as the set of all decision problems for which there exists an algorithm which can be solved in polynomial time. An important point to note is that not all problems that can be solved in polynomial time are P. We are specifically dealing with decision problems here.

NP can be explained as the set of all decision problems that can be solved in polynomial time by a non-deterministic Turing Machine and for which there exists a polynomial time verification algorithm. Let's now understand verification algorithms by analyzing another problem: Prime Factorization.

The problem states that given a composite number, decompose that number as a product of prime numbers. For example, 161 = 7 * 23. For small integers ( something in the order of 10^7 ), a variant of Sieve of Eratosthenes can be used to solve prime factorization problem but as integers get bigger, we start facing serious memory issues making it infeasible to scale. As of today, there is no known algorithm to solve this in Polynomial time complexity ( for all problems ) but verification is still possible. No matter how big the factors are, we can still multiply them to verify whether the product is equal to the original composite number, making this an NP problem. RSA, a public-key cryptosystem uses this problem to secure data transmission.

For a decision problem to be NP-Complete, it should satisfy two conditions:

1. It is in NP.
2. Any problem in NP is reducible to this problem in polynomial time complexity.

Any problem which only satisfies the 2^nd point can be termed as an NP-Hard problem. To visualize this in a better manner think of NP-Complete being at the boundary of NP and NP-Hard problems. The below image will help visualize these concepts:

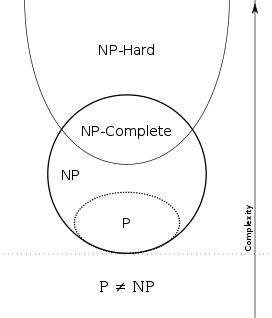
A classic example of a NP-Complete problem would be that of 3-SAT problem. 3-SAT problem is a satisfiability problem which states that given a boolean expression ( supporting AND, OR, NOT, variables and parentheses ) in CNF ( Conjunctive Normal Form ) such that every clause contains exactly 3 literals, does there exist some combination of these literals ( in True or False Form ) such that the expression becomes TRUE ? Check the following equation : ( x1 ∨ x2 ∨ x3 ) ∧ ( x4 ∨ !x5 ∨ x6 ). For this particular equation we can verify that with values like ( T,T,T,T,F,T ), the expression becomes T.

Before I explain why 3-SAT is NP-Complete, I want to share a secret sauce. It turns out that we do not need to reduce every problem in NP to check for NP-Completeness. If are able to reduce an existing NP-Complete problem to this problem, we will be able to satisfy the 2^nd condition. Note that by satisfying the 2^nd condition we can't decisively say that problem is NP-Complete. For that the 1^st condition must be satisfied. 3-SAT is NP-Complete as it can be verified in Polynomial time for any number of literals and we can reduce the unrestricted SAT problem to this problem. ( See the following link for more intuition ).

Fun Fact: SAT problem was the 1^st problem proved to be NP-Complete in 1971 by Stephen Cook.

An example of NP-Hard problem would be the Halting Problem described earlier. SAT problem can be reduced to Halting Problem in polynomial time, but being an undecidable problem, it is not in NP class.

Lastly, the question of whether P=NP has fascinated many. The problem asks whether a problem which can be verified in polynomial time, be solved in polynomial time. To this date this is an unsolved problem mainly because we haven't been able to prove P=NP or it contradicting statement P≠NP.

I hope you found this post increase your curiosity and imagination. Computer Science is truly a breathtaking subject!

Update (16/03/20): I just found this hilarious comic -

Created by XKCD, licensed under CC BY-NC 2.5
Knapsack problem and Travelling salesman problem

←